Proszę o pomoc!!! tępy śrubokręt: W trójkąt równoramienny, którego boki mają długości 10, 13 i 13, wpisano okrąg. Oblicz długość odcinka łączącego punkty styczności okręgu z ramionami tego trójkąta.

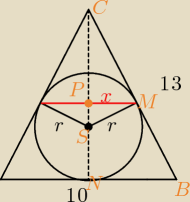
Artur z miasta Neptuna: h_Δ = 12 (z pitagorasa) P_Δ = 60

	2P		120		10
r =		=		=
	10+13+13		36		3

trójkąt CMS jest podobny do trójkąta CNB (takie same kąty), czyli:

r		CM
	=		⇔ CM = 8
5		12

trójkąt CPM jest podobny do trójkąta CNB (takie same kąty), czyli:

PM		CM		PM		8		40
	=		⇔		=		⇔ PM =
5		13		5		13		13

	80
x = 2*PM =
	13

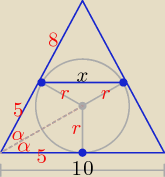Bogdan: Zastosuj twierdzenie o podobieństwie trójkątów.

Bogdan:

	x		10
czyli		=		i tyle
	8		13

tępy śrubokręt: dzięki wielkie!

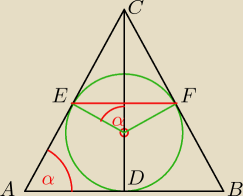Skipper: ICDI=12 S_ΔABC=30

	(10+13+13)r
ale też SΔABC=		=18r
	2

r=5/3 ... alej chyba z góreczki